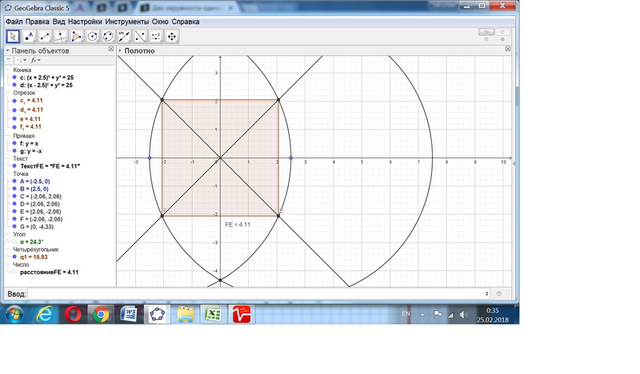
Примем начало координат в центре квадрата.
Тогда его диагонали будут включать уравнения прямых у = х и у = -х.
Уравнения окружностей:
(х + (R/2))² + y² = R² и (х - (R/2))² + y² = R².
Вершины квадрата будут в точках пересечения окружностей с прямыми у = х и у = -х.
Подставим в уравнения вместо у значение х, а R примем равным 1.
Получим квадратное уравнение:
8х² + 4х - 3 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=4^2-4*8*(-3)=16-4*8*(-3)=16-32*(-3)=16-(-32*3)=16-(-96)=16+96=112;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√112-4)/(2*8)=(√112-4)/16=√112/16-4/16=√112/16-0.25 = (√7 - 1)/4 ≈ 0.41143782776615;x_2=(-√112-4)/(2*8)=(-√112-4)/16=-√112/16-4/16=-√112/16-0.25 ≈ -0.91143782776615. Отрицательное значение отбрасываем, так как эта точка выходит за пределы общей части окружностей.
Получаем ответ: сторона квадрата равна двум длинам от нуля до плюс-минус х, то есть а = 2*((√7 - 1)/4)*R ≈ 0,8228757R..