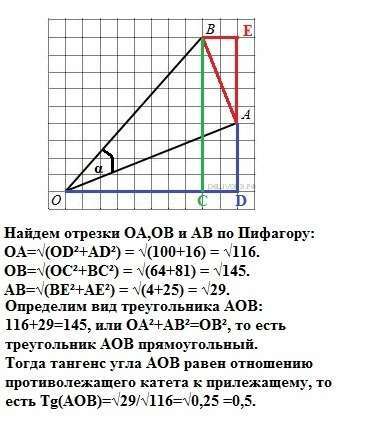
Найдем отрезки ОА,ОВ и АВ по Пифагору:
ОА=√(OD²+AD²) = √(100+16) = √116.
ОB=√(OC²+BC²) = √(64+81) = √145.
AB=√(BE²+AE²) = √(4+25) = √29.
Определим вид треугольника АОВ:
116+29=145, или ОА²+АВ²=ОВ², то есть треугольник АОВ прямоугольный.
Тогда тангенс угла АОВ равен отношению противолежащего катета к прилежащему, то есть Tg(AOB)=√29/√116=√0,25 =0,5.