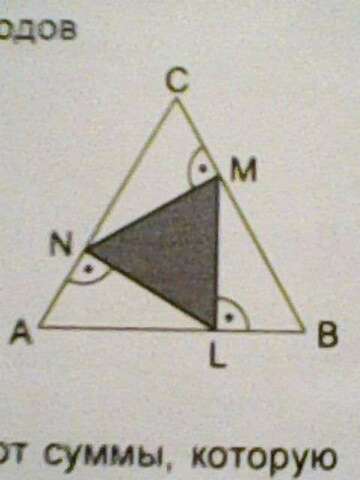
/Задачка из эстонской олимпиады Кенгуру, 7-8 класс, 5 баллов/Точки L, M и N лежат **...

Question

/Задачка из эстонской олимпиады Кенгуру, 7-8 класс, 5 баллов/

Точки L, M и N лежат на сторонах равностороннего треугольника ABC так, что отрезок ML перпендикулярен стороне AB, NM перпендикулярен стороне BC, а LN перпенликулярен стороне AC. Площадь треугольника ABC равна 36. Найди площадь треугольника LMN.
А: 9 B: 12 C: 15
D: 16 E:18
Желательно с объяснением.

---

Answer 1

Так как треугольник правильный, то все его углы равны 60°.
Рассмотрим треугольник MLB. Угол LBM=60°, тогда угол BML=30°.
Пусть LB=х. Тогда MB=2х, так как катет, лежащий против угла в 30°, равен половине гипотенузы. По теореме Пифагора найдем ML:

Сторона исходного треугольника равна:

По построению, треугольник LMN правильный, значит он подобен с треугольником ABC.
Площади подобных треугольников относятся как квадрат коэффициента пропорциональности:

Ответ: 12