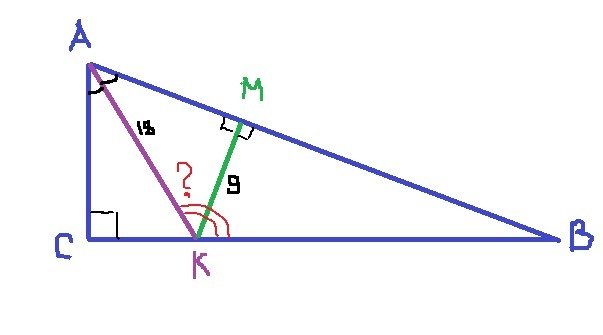
Дано:
Δ АВС
∠С = 90°
АК - биссектр.
АК = 18 см
КМ = 9 см
Найти: ∠АКВ
Решение.
Т.к. расстояние от точки измеряется по перпендикуляру, то опустим его из (·) К на гипотенузу АВ и обозначим это расстояние КМ.
Рассмотрим полученный Δ АКМ, Т.к. ∠АМК = 90°,то АК гипотенуза, а КМ - катет. Поскольку, исходя из условия, катет КМ = 9/18 = 1/2 АК, то ∠КАМ = 30°.
Т.к. по условию АК - биссектриса, то ∠САК =∠КАМ = 30°
Рассмотрим ΔАКС. По условию ∠АСК = 90°; а∠САК = 30°, значит, ∠АКС = 180° - 90° - 30° = 60°
Искомый ∠АКВ - смежный с ∠АКС, значит, ∠АКВ = 180° - ∠АКС = 180° - 60° = 120°
Ответ: 120°