45°.
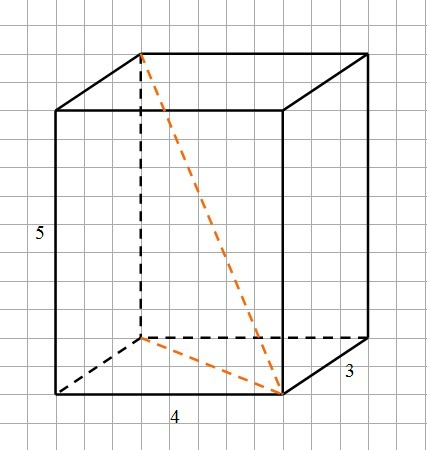
Угол наклона диагонали параллелепипеда к плоскости наименьшей его грани, - это угол между диагональю параллелепипеда и диагональю основания 4х3.
Длина диагонали меньшего основания:
d = √(3²+4²) = √25 = 5
Так как высота параллелепипеда - 5, то имеем прямоугольный равнобедренный треугольник с диагональю параллелепипеда, в качестве гипотенузы, диагональю меньшего основания, в качестве первого катета (5) и высотой параллелепипеда, в качестве второго катета (5). В равнобедренном прямоугольном треугольнике углы при гипотенузе равны 45°