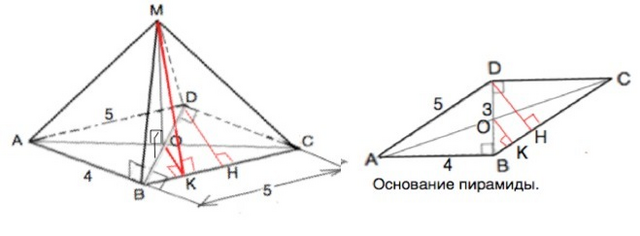
Площадь полной поверхности пирамиды (обозначим её МАВСD)
состоит из суммы площадей всех граней.
Противоположные боковые грани равны по трём сторонам.
Так как МО перпендикулярна плоскости основания, а ВD⊥АВ и CD, то ОВ – проекция наклонной МВ.
По т.о 3-х перпендикулярах МВ⊥АВ.
Диагонали параллелограмма точкой пересечения делятся пополам ⇒. ОВ=1,5.
Высота пирамиды МО⊥ОВ.
Из ∆ МОВ по т.Пифагора
МВ=√(МО²+ОВ²)=√(4+2,25)=2,5
Ѕ(АМВ)=МВ•АВ:2=2,5•4:2=5 м²
Ѕ(MCD)=S(AMB) ⇒Ѕ(MCD)+S(AMB)=10 м²
Найдём высоту второй пары боковых граней.
а) Высота DHпрямоугольного ∆ BDH (в основании) равна произведению катетов, делённому на гипотенузу.
DH=DB•DC:BC=3•4:5=2,4 м
Проведем ОК⊥ВС
ВO=ОD ⇒ ОК - средняя линия ∆ВDH и равна половине DH.
ОК=1,2 м
ОК - проекция наклонной МК. ⇒ По т.ТПП отрезок МК⊥ВС и является высотой ∆ ВМС
б) Из прямоугольного ∆ МОК по т.Пифагора
МК=√(MO²+OK²)=√(4+1,44)=√5,44
√5,44=√(544/100)=(2√34):10=0,2√34
S(MBC)=BC•MK:2=0,5•5•0,2√34=0,5√34 м²
S(AMD)=S(MBC)⇒ S(AMD)+S(MBC)=2•0,5√34=√34 м²
S(ABCD)=DB•AB=3•4=12 м²
Площадь полной поверхности MABCD:
2•S(AMB)+S(ABCD)+2•S(MBC=10+12+√34=(22+√34)м²