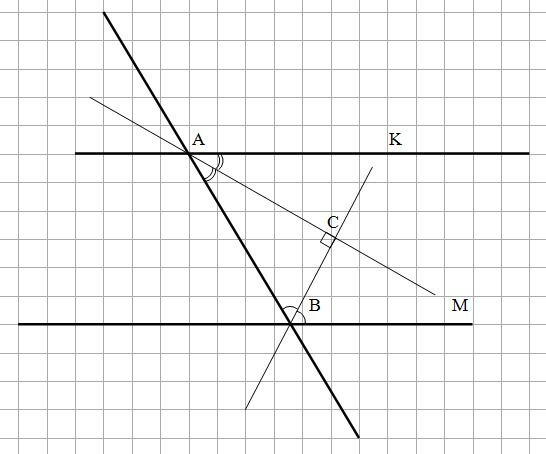
∠КАВ = ∠1
∠АВМ = ∠2
Так как сумма внутренних односторонних углов равна 180°, то:
∠1 + ∠2 = 180°
и 0,5∠1 + 0,5∠2 = 0,5*180 = 90°
Получили треугольник ΔАСВ с углами при основании, составляющими в сумме 90°. Значит, угол при вершине ∠АСВ = 90°.
Следовательно, биссектрисы внутренних односторонних углов, пересекаются под прямым углом, то есть взаимно перпендикулярны.