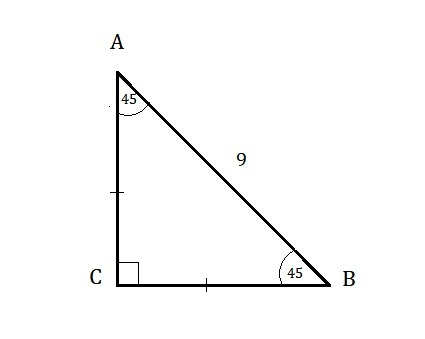
Дано:
ΔАВС - прямоугольный
∠С = 90°
∠А = 45°
АВ = 9
Найти : S aвc - ?
Решение.
Сумма острых углов прямоугольного треугольника равна 90°
∠А + ∠В = 90 ⇒ ∠В = 90 - ∠А ⇒ ∠В = 90 - 45 = 45°
∠А = ∠В = 45° ⇒ Δ АВС - равнобедренный ⇒ АС=СВ=х
По теореме Пифагора:
АС² + СВ² = АВ² ⇒ 2х² = АВ² ⇒ 2x² = 9² ⇒ x² = 81/2 = 40,5
Площадь ΔАВС :
Saвc = ¹/₂ * АВ * СВ ⇒ Sавс = 0,5х² ⇒ Saвc = 0,5 * 40,5 = 20,25
Ответ : Sавс = 20,25