18. В треугольнике АВС АВ=ВС=10 см, АС=12 см. Через точку В к плоскости треугольника...

Question

18. В треугольнике АВС АВ=ВС=10 см, АС=12 см. Через точку В к плоскости треугольника проведен перпендикуляр BД длиной 15 см. Найдите расстояние от точки Д до прямой АС.
19. Диагонали квадрата АВСД пересекаются в точке О. КО - перпендикуляр к плоскости квадрата. КО=4√(2) см. Докажи гс равенство углов, образуемых прямыми КА, КВ, КС и КД с плоскостью квадрата. Найдите эти углы, если периметр АВСД равен 32 см.

Answer 1

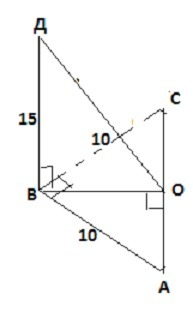
18. ДВ⊥АВС, значит, используя теорему о трех перпендикулярах ⇒ДС⊥АС, ВО⊥АС. Поэтому все элементы находим с помощью т. Пифагора.
АВС- равнобедренный по условию,⇒АО=1/2АС=12/2=6см.
ВО=√(АВ²-АО²)=√(100-36)=8см.
ДО=√(ДВ²+ОВ²)=√(225+64)=√289=17см.
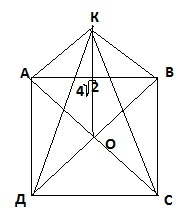
19. Р АВСД=32см⇒АВ=ВС=ДС=АД=32/4=8см.тогда по т. Пифагора
ДВ=√(ДС²+СВ²)=8√2см.ОВ=1/2ДВ=4√2см.⇒КО=ОВ=4√2 и ΔКОВ-равнобедренный, ∠КОВ=90°, значит ∠КВО=45°..
ΔКОВ=ΔКОС=ΔКОД=ΔКОА по первому признаку⇒
∠КВО=∠КСО=∠КДО=∠КАО, что и требовалось доказать..
К решению прикреплены 2 рисунка.

---

---