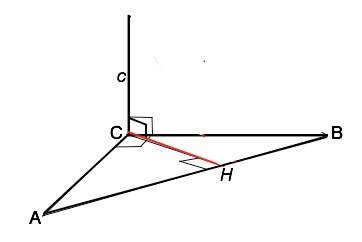
Прямая АВ лежит в плоскости АВС, а прямая с эту плоскость пересекает в точке С, не принадлежащей прямой АВ.
Прямая с и прямая АВ - скрещивающиеся.
Расстояние между скрещивающимися прямыми измеряется длиной их общего перпендикуляра.
Проведем СН⊥АВ.
Прямая с перпендикулярна плоскости АВС, следовательно, перпендикулярна любой прямой в этой плоскости.⇒ с⊥СН
Длина СН - искомое расстояние.
СН⊥АВ и является высотой ∆ АВС.
Из площади прямоугольного треугольника
S=0,5•AC•СB
S=0,5•CH•AB⇒
СН=АС•ВС:АВ
По т.Пифагора АВ= √(AC*+BC*)=√(9+16)=5 дм
СН= 3•4:5=2,4 дм