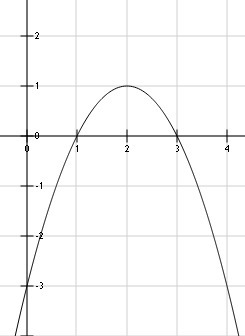
Y=-x²+4x-3
1) Область определения – любое действительное число
D(f) = R
2)
Коэффициент a, стоящий при x², равен − 1. Коэффициент b, стоящий при x, равен 4. Найдем координату x вершины параболы по формуле x₀=-b/2a
x₀=-4/-2 =2
Коэффициент −1, стоящий перед x², есть число отрицательное.
Значит, ветви параболы направлены вниз, и функция сначала возрастает до точки 2, а затем начинает убывать до конца области определения, т.е. до +∞.
Промежутки возрастания и убывания:
(−∞; 2) - функция возрастает;
(2; +∞) - функция убывает.
3) интервалы знакопостоянства
найдём нули функции (точки пересечения графика с осью абсцисс)
решим уравнение f(x)=0
-x²+4x-3=0
D=16-4*3=4


f(x) >0 если х∈(1;3)
f(x) <0 если х∈(-∞;1)∪(3;+∞)<br>