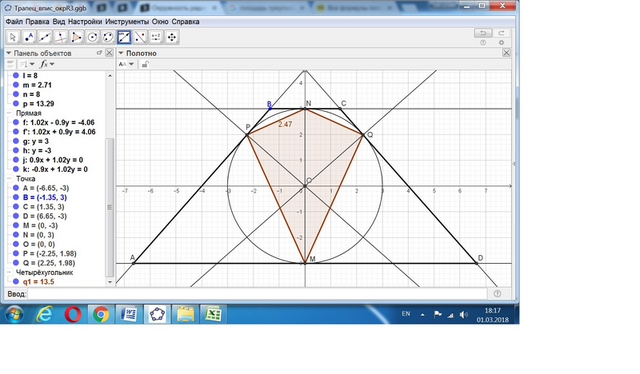
Средняя линия L трапеции, в которую вписана окружность радиуса R, равна: L = S/(2R) = 48/(2*3) = 8.
Боковая сторона такой трапеции равна средней линии.
Находим синус острого угла А:
sin A = 6/8 = 3/4.
Угол PON, как взаимно перпендикулярный с углом А, равен ему.
Тогда отрезок PQ равен:
PQ = 2*R*sinA = 2*3*(3/4) =9/2.
Ответ: площадь S четырёхугольника MPNQ равна:
S = (1/2)*6*(9/2) = 27/2 = 13,5.