V=S(осн)*h/3
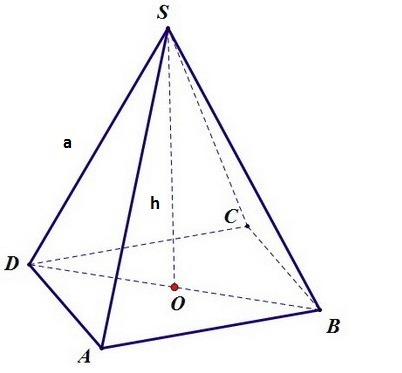
в основании квадрат-необходимо найти сторону основания, и высоту пирамиды
На чертеже диагональное сечение-ΔBDS, по условию он прямоугольный( Его S=12=a^2/2(a-боковое ребро пирамиды), значит а=√24=2√6
DB-гипотенуза прямоугольного треугольника со стороной а, поэтому
DB^2=2a^2=2*24=48; DB=4√3
DB-диагональ квадрата в основании, поэтому сторона основания AB=DB/√2=4√3/√2=2√6
S(осн)=AB^2=(2√6)^2=24
Из ΔDSO найду h, h^2=a^2-(DB/2)^2=24-(2√3)^2=24-12=12
h=√12=2√3
V=24*2√3/3=16√3