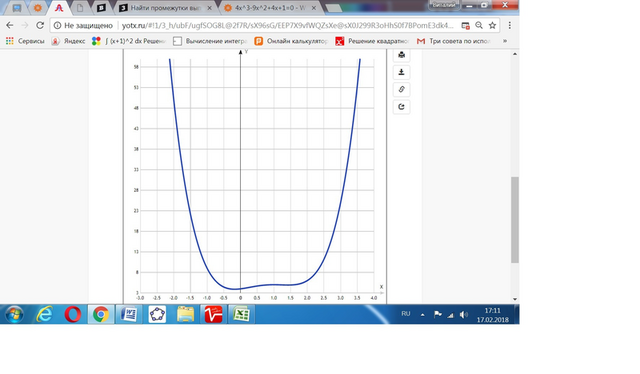
Дана функция f(x)=x^4-3x^3+2x^2+x+4.
Первая производная функции равна:
y' =4x³ - 9x² + 4x + 1.
Вторая производная равна:
y'' = 12x² - 18x + 4.
Приравниваем её нулю:
12x² - 18x + 4 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-18)^2-4*12*4=324-4*12*4=324-48*4=324-192=132;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=√132-(-18))/(2*12)=(√132+18)/(2*12) = = (√132+18)/24=√132/24+18/24=2root132/24+0.75 ≈ 1,228714;x_2=(-√132-(-18))/(2*12)=(-√132+18)/(2*12)=(-√132+18)/24=
= -√132/24+18/24=-√132/24+0.75 ≈ 0,2712864.
Получили 2 точки перегиба графика функции:
х = 1,228714 и х = 0,2712864, и 3 промежутка выпуклости графика.
Находим знаки второй производной на найденных промежутках.
Где
вторая производная меньше нуля, там график функции выпуклый, а где больше -
вогнутый.
x =
0 0,27129
1
1,22871
2
y'' =
4 0 -2
0 16.
Как видим, график на двух промежутках вогнутый: (-∞; ((3/4)-(11/3)^1/2)/4)) и ((3/4)+(11/3)^1/2)/4).
На промежутке (((3/4)+(11/3)^1/2)/4); +∞) график выпуклый.