Задача 1
ДАНО
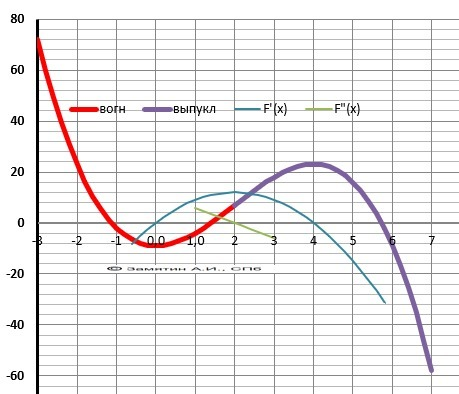
Y= -x³ + 6*x² + 9
РЕШЕНИЕ
График к задаче в приложении.
1) Первая производная - точки экстремумов
Y'(x) = -3x²+ 12*x = - 3*x*(x-4) = 0
Корни: х1 = 0, х2 = 4 - график
Максимум - Y(4) = (самостоятельно)
Минимум - Y(0) = +9
Область монотонности:
Возрастает - между корнями: Х∈[0;4]
Убывает - вне корней - Х∈(-∞;0]∪[4;+∞)
2) Вторая производная - точка перегиба.
Y"(x) = - 6*x+ 12 = - 6*(x-2) = 0
Корень: х = 2
Убывает - X∈(-∞;2] и возрастает X∈[2;+∞)
Задача 2
ДАНО
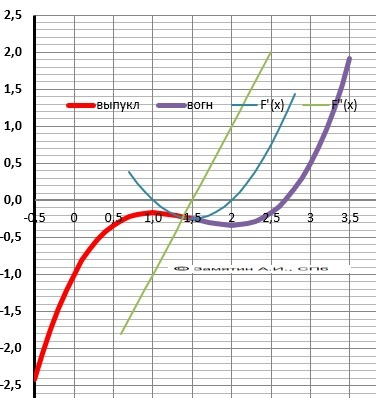
Y= x³/3 - 3/2*x² +2*х -1
РЕШЕНИЕ
График к задаче в приложении.
1) Первая производная - точки экстремумов
Y'(x) = x² -3x+ 2 = (x-2)*(x-1) = 0
Корни: х1 = 1, х2 = 2 - график
Максимум - Y(1) = - 1/3
Минимум - Y(2) = -1/6
Область монотонности:
Убывает - между корнями: Х∈[1;2]
Возрастает - вне корней - Х∈(-∞;1]∪[2;+∞)
2) Вторая производная - точка перегиба.
Y"(x) =2*x - 3 = 0
Корень: х = 1,5
Возрастает - X∈(-∞;1,5] и убывает X∈[1,5;+∞)