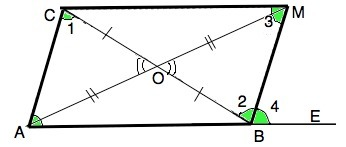
Дано: АВ=ВС. ⇒ ∆ АВС - равнобедренный. (См. рисунок приложения)
∆ АОС=∆ ВОМ по первому признаку ( АО=МО и ВО=СО по условию, углы при О между ними равны, как вертикальные).⇒
АС=ВМ.
Аналогично доказывается равенство ∆ СОМ=∆ АОВ
СМ=АВ⇒ СМ=ВС.
∆ МСВ = ∆ АСВ - равнобедренные и равны. Их углы при АС и ВМ равны. .
В четырехугольнике АВМС противоположные стороны равны. ⇒
АВМС ⇒ параллелограмм по определению.
АС║ВМ, ВС – секущая. Накрестлежащие ∠1=∠2
СМ║АВ, МВ – секущая. Накрестлежащие ∠3=∠4
Но в равнобедренном ∆ МСВ ∠2=∠3.
Следовательно, ∠2=∠4, и ВМ - биссектриса угла СВЕ, ч.т.д.