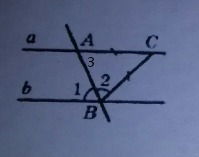
АС = ВС по условию ⇒ ΔАВС - равнобедренный.
В равнобедренном треугольнике углы при основании равны ⇒ ∠2=∠3
∠1 = ∠2 и ∠3 = ∠2, следовательно ∠1 = ∠3
∠1 и ∠3 - накрест лежащие углы при прямых а и b и секущей АВ. Из равенства накрест лежащих углов следует, что а || b. Что и требовалось доказать.