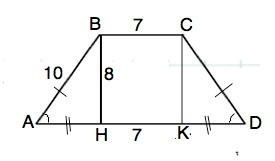
Опустим из вершин В и С высоты ВН и СК.
Углы при основании равнобедренной трапеции равны, боковые стороны равны ⇒ прямоугольные треугольники, отсекаемые от трапеции высотами из тупых углов, равны по углу и гипотенузе.
Из ∆ АВН по т.Пифагора АН=√(AB²-BH²)=√(100-64)=6 см.
АD=AH+HK+KD=6+7+6=19 см
Площадь трапеции равна произведению полусуммы оснований на высоту.
S=0,5•(BC+AD)•BH=0,5•(7+19)=13•8=104см²