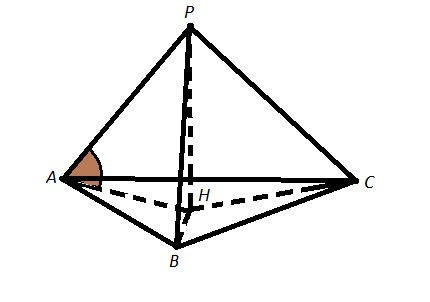
Так как РН⊥пл. АВС и точка Р равноудалена от вершин ΔАВС, то точка Н есть центр описанной около ΔАВС окружности.
Найдём радиус описанной окружности по формуле R=abc/4S ,
где R=AH=BH=CH .
S найдём по формуле Герона.
p=P/2=(6+25+29)/2=60/2=30
S=√p(p-a)(p-b)(p-c)=√(30·24·5·1)=√3600=60
R=(6·25·29)/(4·60)=4350/240=145/8=18,125
Рассм. ΔАРН. ∠РАН - угол между АР и пл. АВС, так как РН⊥ пл.АВС ⇒
РН⊥АН , ∠PHA=90°.
АН - проекция наклонной АР на пл.АВС,РН=15.
tg∠PAH=PH/AH=15/18,125=15/(145/8)=(15·8)/145=120/145=24/29
∠PAH=arctg24/29