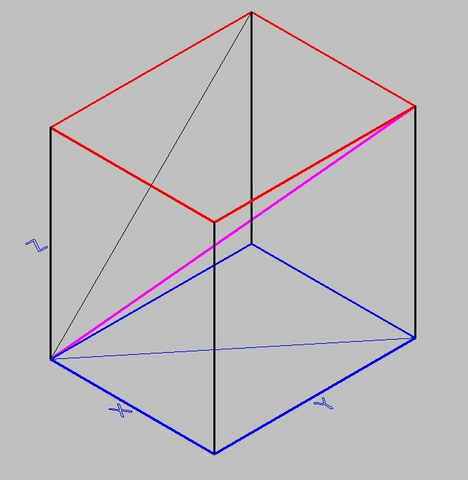
Пусть с нижней синей гранью угол 45°
проекция диагонали на основание равна √(x²+y²)
tg(45°) = z/√(x²+y²) = 1
z/√(x²+y²) = 1
z²/(x²+y²) = 1
z² = x² + y²
и с задней чёрной гранью угол 30°
проекция диагонали на заднюю грань √(x²+y²)
tg(30°) = x/√(y²+z²) = 1/√3
x/√(y²+z²) = 1/√3
3x² = y² + z²
подставим из прошлого пункта
3x² = y² + x² + y²
2x² = 2y²
x = y
z² = 2x²
z = x√2
и длина диагонали
l² = x² + y² +z² = x² + x² +2x² = 4x²
x = l/2
y = l/2
z = l/√2
Объём
V = x*y*z = l/2*l/2*l/√2 = l³/(4√2)