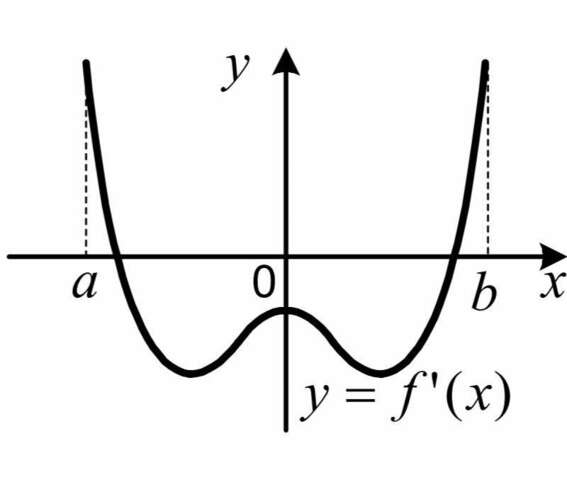
Функция у=f(x) определена на промежутке [а; b] и имеет производную в каждой точке области определения. На рисунке изображён график производной (т.е. у=f'(x)). Сколько промежутков убывания имеет функция у=f(x)?
P.S. Ответ, пожалуйста, с подробным объяснением рассуждений!