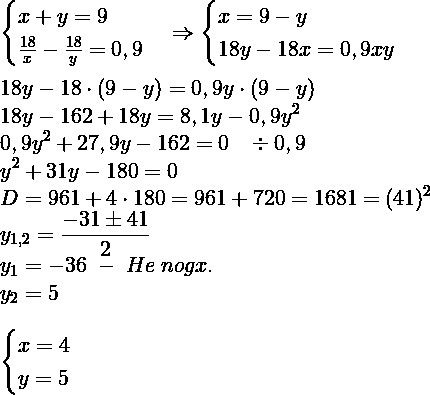54 мин = 54/60 = 9/10 = 0,9 часа
Скорость первой группы x км/ч, второй - y км/ч. За 2 часа навстречу друг другу прошли 18 км, то есть
(x+y)*2 = 18
или
x+y = 9
Первая группа прошла весь путь за 18/x часов, вторая за 18/y часов. Пусть вторая прошла весь путь на 0,9 часа быстрее, тогда
18/x-18/y = 0,9
Составим и решим систему уравнений: