S(полн)=S(осн)+S(бок)
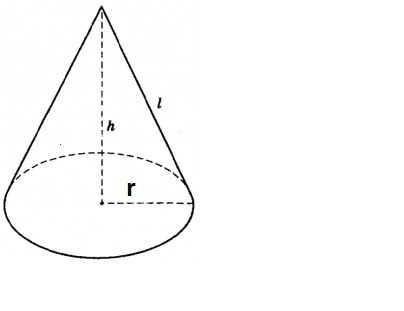
если r-радиус основания, то S(осн)=pi*r^2
S(бок)=pi*r*R, где R-образующая конуса и радиус сектора
S(бок)=pi*R^2/6
мне необходимо найти связь r и R, я сделаю это через длину окружности основания l=2pir и длину дуги сектора.( они будут равны)l=2piR/6
приравнивая правые части , получу
2pir=2piR/6; r=R/6;R=6r
подставляя все в общую площадь поверхности получу
pir^2+pir*6r=7pir^2=45pi; 45=7r^2; r=√(45/7)
h^2=(6r)^2-r^2=35r^2; h=r*√35=15
V=pi*(45/7)*15/3=225pi/7