Две окружности пересекаются в точках А и В. Через точки пересечения окружностей проведены...

Question

Две окружности пересекаются в точках А и В. Через точки пересечения окружностей проведены прямые, которые пересекаются в точке С и пересекают окружности в точках М, К, Р и Е. Докажите, что треугольники СКР и СМЕ подобны. Найдите СК и СР, если МЕ = 9 см, КР = 6 см, СМ = 12 см, СЕ = 15 см.

Answer 1

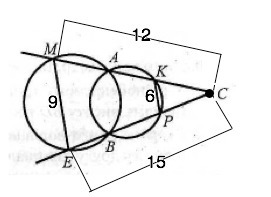
По теореме: Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на ее внешнюю часть. (как следствие теоремы о касательной и секущей из одной точки).  

Для меньшей окружности 

СА•СК=СВ•СР, откуда

СА:СВ=СК:СР

Для большей окружности 

СЕ•СВ=СМ•СА, откуда 

СМ:СЕ=СА:СВ. ⇒

СК:СР=СМ:СЕ ⇒СК:СМ=СР:СЕ

Второй признак подобия треугольников. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то треугольники подобны. 

Из подобия ∆ СКР и Δ СМЕ следует отношение 

СК:СМ=РК:ЕМ

СК:12=6:9⇒ СК=8 см. 

и 

СР:СЕ=КР:МЕ 

⇒ СР=10 см

---