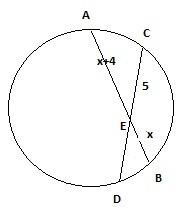
Если две хорды окружности, AB и CD пересекаются в точке Е, то произведение отрезков одной хорды равно произведению отрезков другой хорды: АЕ*ВЕ=СЕ*DE
Пусть ВЕ=х, то АЕ=х+4, СЕ=5см, DE=CD-СЕ=17-5=12см⇒
(х+4)*х=5*12
х²+4х-60=0
D=b²-4ас=16-4*(-60)=256, х1=(-4-√256)/2*1=-10-не используем
х2=(-4+√256)/2*1=12/2=6см⇒
ВЕ=6см, то АЕ=6+4=10см.
Проверяем: АЕ*ВЕ=СЕ*DE, 10*6=12*5; 60=60
Ответ: ВЕ=6см, АЕ=10см.