В треугольнике abc точка d середина стороны bc. точка делит сторону abв отношении 1 к 2...

Question

В треугольнике abc точка d середина стороны bc. точка делит сторону abв отношении 1 к 2 очитая от a точка q делит сторону bc в отношении 2 к 5 считая от b найдите отношение площадей треугольников rdq и abc

Answer 1

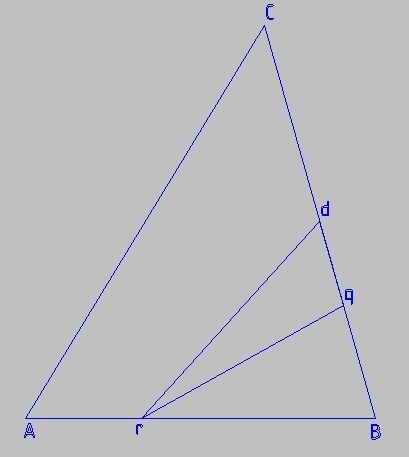
В качестве основания для вычисления площади используем сторону ВС
qd = BC-Cd-Bq = BC-1/2*BC-2/7*BC = BC(14-7-4)/14 = 3/14*BC
Высота от точки А к стороне BC больше высоты от точки r к стороне BC в полтора раза
S(rdq) = 1/2*dq*h(r к ВС) = 1/2*3/14*BC*2/3* h(A к ВС) = 1/2*BC*h(A к ВС)*1/7
Ответ - площадь дочернего треугольника в 7 раз меньше площади исходного

---

Comments

S(rdq) = 1/2*dq*h(r к ВС) = 1/2*3/14*BC*2/3* h(A к ВС) = 1/2*BC*h(A к ВС)*1/7

---

Большой в 7 раз больше!