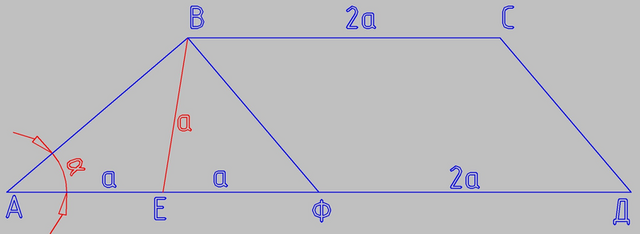
АЕ/ЕД = 1/3
Т.е. всего основание АД состоит из 4-х частей, из которых АЕ - одна часть, ЕД - три части.
Меньшее основании в два раза меньше, это две части.
ВФ - отрезок, параллельный СД
АФ = АД - ВС
и длина АФ составляет две части, получается, что точка Е - медиана треугольника АВФ
В треугольнике АВФ угол А = α, угол Ф = 90-α, угол В = 90°
В прямоугольном треугольнике медиана прямого угла является ещё и радиусом описанной окружности, и в два раза короче гипотенузы.
Получается, что данная нам по условию величина a - это те самые части, из которых состоят основания
ВС = 2а
АД = 4а
Высота трапеции совпадает с высотой треугольника АВФ
Гипотенуза АФ
АФ = 2а
Катет АВ
АВ/АФ = cos(α)
АВ = АФ*cos(α) = 2а*cos(α)
Высота из точки В к основанию АД
h = АВ*sin(α) = 2а*cos(α)*sin(α) = а*sin(2α)
Площадь трапеции
S = 1/2*(АД + ВС)*h = 1/2*(4а+2а)*а*sin(2α) = 3a²*sin(2α)
При
а=17,3
α = 40 23/60°
S = 3*17,3²*sin(2*(40 23/60°)) ≈ 886,82469