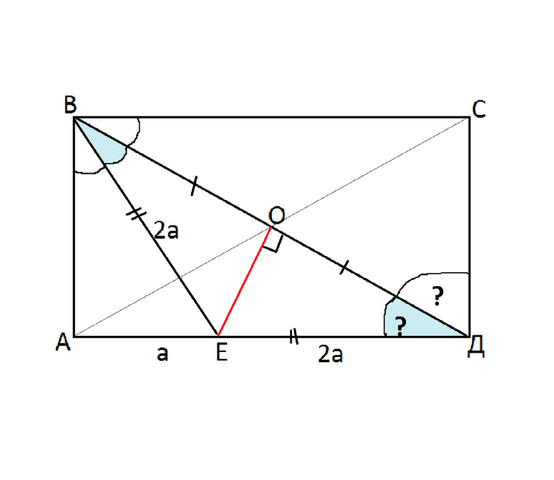
Как известно, диагонали прямоугольника равны и точкой пересечения делятся пополам.
Нарисуем прямоугольник АВСД, проведем в нем диагонали.
Точку пересечения диагоналей обозначим О.
Проведем ОЕ перпендикулярно ВД.
Соединим В и Е.
В треугольнике ВЕД ВО=ОД по построению.
ОЕ в нем медиана и высота.
Треугольник ВЕД - равнобедренный.
Рассмотрим прямоугольный треугольник АВЕ
ВЕ=2АЕ ( из равенства ВЕ=ЕД)
Синус угла АВЕ=а:2а=0,5, и это синус угла с градусной мерой 30°.
Второй угол, на который диагональ ВД поделила угол АВС, равен
∠СВЕ=90°-30°=60°
Остальные углы прямоугольника делятся диагоналями также на углы 30° и 60°.