1)
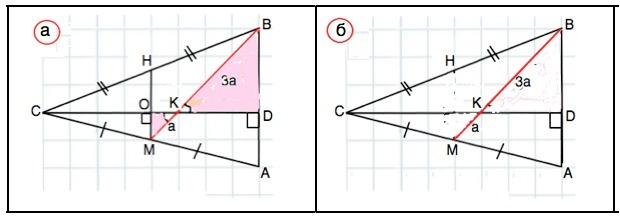
а) Проведем МН параллельно АВ. СМ=АМ⇒ МН средняя линия ∆ АВС.
∠СОМ=∠СDA=90° как соответственные.
В прямоугольных ∆ ОКМ и ∆ ВКD углы при К равны (вертикальные)⇒ Эти треугольники подобны с k=BK:MK=3:1
Тогда DB:OM=3:1
Для удобства примем BD=3. Тогда ОМ=1
ОМ - средняя линия ∆ ADC ⇒ AD=2•OM=2 ⇒
AD:DH=2:3
——————
Или, если Вы знакомы с т.Менелая.
б) По т.Менелая для ∆ АВМ:
АD:DB•BK:KM•MC:CA=1
AD/DB•3/1•1/2=1—
AD/DB=2/3
=======================================
2)
В равнобедренном треугольнике АВС к боковой стороне ВС проведена медиана АК=12 см . Высота ВН пересекает медиану в т.Р. Угол КАС=30° Найдите ВН.
Высота равнобедренного треугольника - его медиана.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒
АР:РК=2:1 ⇒ АР=12²3•2=8 см
В прямоугольном ∆ АРК катет РН противолежит углу 30° и равен половине гипотенузы АР.
РН=4, ВР=2•РН=8 ⇒ ВН=12 см