1) ООФ: x∈R
2) y(-x) = 3*(-x)³-(-x)^4 = -3x³-x^4 ≠ y(x), ≠ -y(x) - функция общего вида (не чётная, не нечётная).
3) пересечение с осями
С OY, x=0:
y=0
(0; 0)
С OX, y=0:
3x³-x^4 = 0
x³(3-x) = 0
x = 0, x = 3
(0; 0), (3; 0) - две точки
4) асимптоты:
вертикальных нет.
горизонтальные:
lim(3x³-x^4) = -∞ - горизонтальных нет
наклонные:
lim(3x²-x³) = -∞ - наклонных нет.
5) крит. точки, интервалы возрастания и убывания:
y' = 9x²-4x³
9x²-4x³ = 0
x²(9-4x) = 0
x = 0, x = 9/4 = 2,25
При x∈(-∞; 0) y'(x) > 0 - функция возрастает
При x∈(0; 2,25) y'(x) > 0 - функция возрастает
При x∈(2,25; +∞) y'(x) < 0 - функция убывает
(2,25; 0) - точка максимума.
6) точки перегиба, интервалы выпуклости и вогнутости:
y'' = 18x-12x²
18x-12x² = 0
6x(3-2x) = 0
x = 0, x = 3/2
При x∈(-∞; 0) y''<0 - функция выпукла<br>При x∈(0; 3/2) y''>0 - функция вогнута
При x∈(3/2; +∞) y''<0 - функция выпукла<br>y(0) = 0
y(3/2) = 81/16 ≈ 5
(0; 0), (3/2; 5) - точки перегиба.
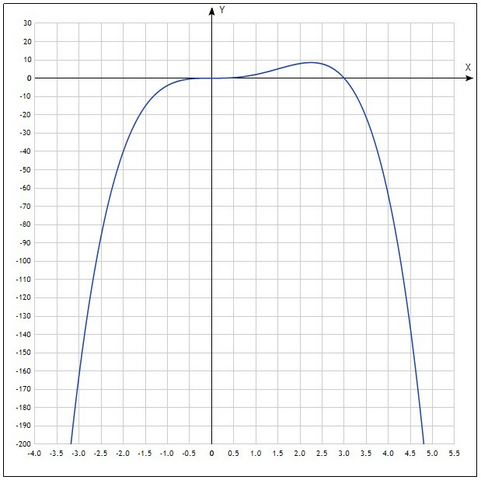
7) график - см. рисунок