Задачу можно решать разными способами.
Ниже предложены два с самыми простыми, на мой взгляд, вычислениями.
1)
Формула медианы треугольника
М=0,5•√(2a²+2b²-c²). где а и b стороны, между которыми проведена медиана, с - сторона, к которой она проведена.
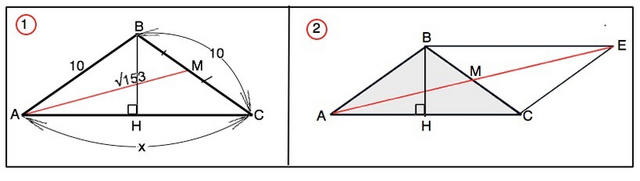
Обозначим треугольник АВС, АВ=ВС=10, АС=х, медиана АМ=√153
√153=0,5•√(200+2x² -100)
Возведя обе части уравнения в квадрат, получим
153= 0,25•(100+2х²) откуда
153:0,25=100+2х²
2х²=512⇒
х²=256
х=16
ВН - медиана, ⇒АН=СН=8
По свойству медианы равнобедренного треугольника, проведенной к его основанию, ВН - его высота. ⇒
∆ АВН прямоугольный.
По т.Пифагора ( или заметив, что ∆ АВН - египетский) находим длину медианы ВН=6.
Или
2)
Продлим медиану АМ на её длину до точки Е, соединим В и С с т.Е. Четырехугольник АВЕС - параллелограмм ( по признаку: диагонали в т.пересечения делятся пополам).
По свойству параллелограмма
d²+D²=(2•(a²+b²), где d и D - диагонали параллелограмма, , а и b - его стороны.
ВС²+АЕ²=2•(АВ²+АС²)
АЕ=2•√153 ⇒
100+612=2•(100+АС²) ⇒
АС=16
Медиана ВН находится, как в первом решении. .