Подобные задачи часто встречаются. Для вычисления площади фигур, изображенных на клетчатой бумаге, существует несколько способов.
1) Делят данную фигуру на меньшие, чтобы их вершины совпадали с точками пересечения линий клеточек, размеры которых легко вычислить, и складывают их площади.
2) Строят около фигуры другую так, чтобы получилась фигура большего размера, (обычно прямоугольник), чью площадь легко вычислить, затем находят фигуры, окружающие данную, чьи площади тоже легко вычислить, и из большей площади вычитают площади "лишних", получая тем самым искомую площадь.
Для вычисления площади данного треугольника первый способ не подходит.
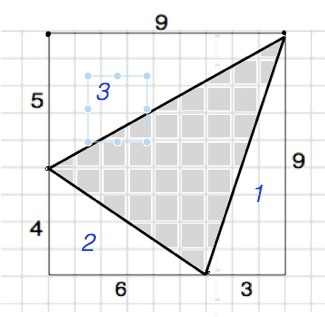
Нужно описать вокруг треугольника прямоугольник. Здесь это квадрат площадью S(кв)=9²=81
Вычисляем площади 3-х треугольников, примыкающих к данному.
Ѕ1=9•3:1=13,5 см²
Ѕ2=6•4:2=12 см²
Ѕ3=5•9:2=22,5 см²
Ѕ(АВС)=Ѕ(кв)-(Ѕ1+Ѕ2+S3)=81-(13,5+12+22,5)=81-48=33 см²
-----------
Для вычисления площади фигур на клетчатом фоне существует формула Пика. Если интересует, её легко найти в сети.