ПОМОГИЕ С ГЕОМЕТРИЕЙ!!!!!!!! В правильной четырехугольной пирамиде боковое ребро образует...

Question

ПОМОГИЕ С ГЕОМЕТРИЕЙ!!!!!!!!
В правильной четырехугольной пирамиде боковое ребро образует со стороной основания угол β. Отрезок, который соединяет центр вписанной в боковую грань окружности с вершиной основания этой грани, равен I. Определить боковую поверхность пирамиды.

Answer 1

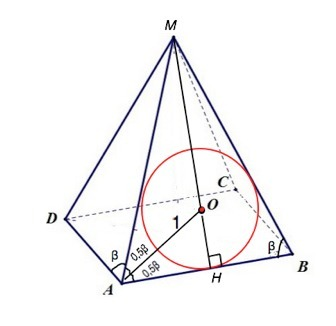
Пирамида правильная, поэтому боковые грани - равные равнобедренные треугольники. 

Центр окружности, вписанной в треугольник, лежит в точке пересечения биссектрис.

 Грань АМВ: треугольник, в котором АВ - основание,  а его высота МН, поскольку высота равнобедренного треугольника ещё биссектриса и медиана,  делит АВ пополам.

  АН=НВ, 

Апофема МН=АН•tgβ

AH=ОА•cos(0,5β)=cos(0,5β)⇒

MH=cos(0,5β)•tgβ

SAMB=MH•AH=cos(0,5β)•cos(0,5β)•tgβ=cos²(0,5β)•tgβ

S(бок)=4•cos²(0,5β)•tgβ

---