Функция y=f(x) - кусочная, состоящая из трех участков. На каждом участке имеется однотипная функциональная зависимость вида y(x)=kx+b, графиком которой является прямая линия. Следовательно, график функции будет состоять из трех отрезков прямых.
Для построения прямой линии необходимо иметь две точки. Пусть первая из точек принадлежит границе интервала определения функции, а вторую выберем произвольно.
1. x<-5 определяет интервал [-∞;5), y=x-3<br>y(-5) = -5-3 = -8; y(-7) = -7-3 = -10 (-7 - выбрано произвольно на интервале)
2. -5≤x≤2 определяет интервал [-5;2], y=-1.5x-2.5
y(-5) = -1.5×(-5)-2.5 = 5; y(2) = -1.5×2-2.5 = -5.5
3. x>2 определяет интервал (2;∞], y=2.5x-3.5
y(2) = 2.5×2-3.5 = 1.5; y(4) = 2.5×4-3.5 = 6.5 (4 - выбрано произвольно).
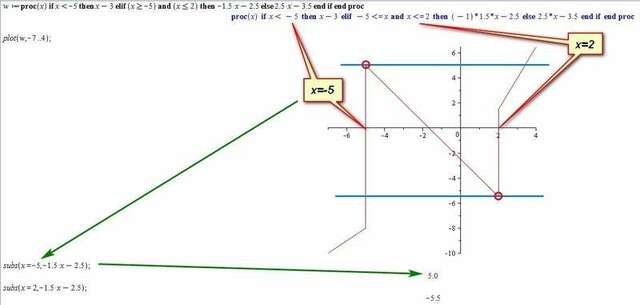
Строим графики по полученным точкам. При х=-5 и x=2 функция имеет скачки, но разрывов нет. (вложение 1)
Прямая y=a проходит параллельно оси абсцисс. Чтобы она имела с графиком ровно две общие точки, она должна располагаться так, как указано во вложении 1 голубыми линиями. Видно, что одна из точек каждой прямой (помечена красным кружком) совпадает с границами второго интервала. А эти границы заданы: -5 и 2.
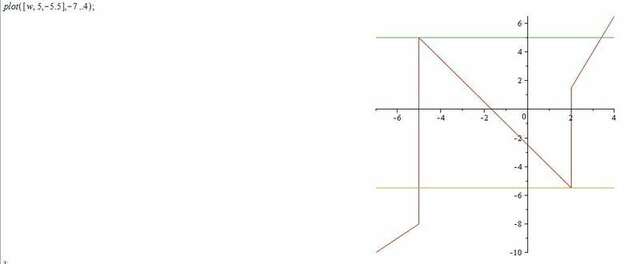
Проводим эти линии (вложение 2) параллельно оси абсцисс.