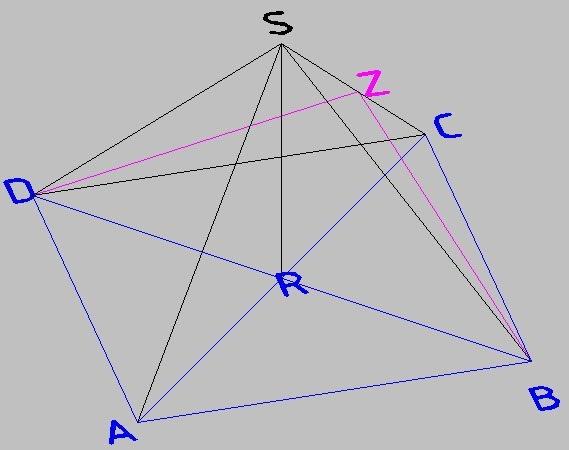
ZB и ZD - высоты боковых сторон, их длина
h = 1*cos(60°) = √3/2
BD - диагональ основания
d = √2
И угол DZB найдём по теореме косинусов
d² = h² + h² - 2h²*cos(∠DZB)
d² = 2h² - 2h²*cos(∠DZB)
(√2)² = 2*(√3/2)² - 2*(√3/2)²*cos(∠DZB)
2 = 2*3/4 - 2*3/4*cos(∠DZB)
2 = 3/2 - 3/2*cos(∠DZB)
1/2 = -3/2*cos(∠DZB)
cos(∠DZB) = -1/3
∠DZB = arccos(-1/3) ≈ 109,5°