ДАНО
F(x) = 1/(1+x²)
РЕШЕНИЕ
1 - область определения - наименьшее значение в знаменателе при Х=0 функция Y= 1. Деления на 0 - нет. Функция непрерывная.
D(x) - X∈(-∞;+∞) - ОТВЕТ
2. - функция чётная - Y(-x) = Y(x). Поэтому сразу пишем вывод - значения функции при противоположных значениях аргумента - РАВНЫ.
F(-10)=F(10) = 1/111
F(-3)=F(3) = 1/10
F(-1) = F(1) = 1/2
F(0) = 1
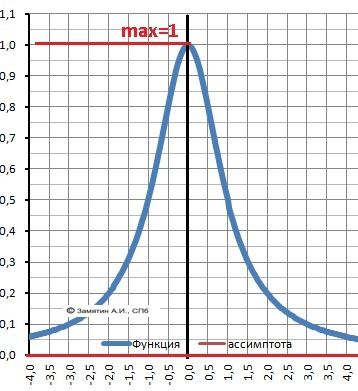
3. Наибольшее значение - при Х=0 значение F(0) = 1 - слишком просто.
Локальный экстремум - максимум или минимум находится в корнях первой производной функции.

Решение: x = 0, значение F(0)=1 - максимум - ОТВЕТ
4. Находим горизонтальную асимптоту:
Значения: F(-∞) = 0 и F(+∞) = 0.
Функция стремится к 0, но никогда не равна 0, и тем более, не может быть отрицательной.
5. Область значений - Е(у) - У∈(0;1].
Важно: круглая скобка - не равна 0, квадратная скобка - равна 1.
График функции в приложении - подарок к расчету.