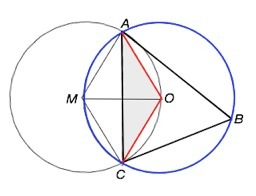
∆ АВС вписанный, т.к. около него описана окружность. Радиусом этой описанной окружности, где О - центр, являются отрезки ОА и ОС.
Радиусу этой окружности равен радиус другой окружности, проходящей через точки А, С, О,
Следовательно, центр М этой второй окружности лежит на первой, отрезок МО – общий радиус для обеих окружностей.
МО=АО=МА -- четырехугольник АМСО - ромб, а треугольник МАО – равносторонний.⇒
Угол МАО=60°
Сумма углов параллелограмма, прилежащих к одной стороне, 180°.
Ромб - параллелограмм.
Тупой угол АОС ромба равен 180°-60°=120° и является центральным для окружности, описанной около ∆ АВС.
Вписанный угол В опирается на ту же дугу, что центральный АОС и равен его половине. Угол В=60°.