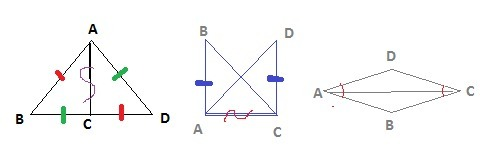
А) По условию задачи АВ=СD, BC=AD, AC-общая сторона⇒ΔABC=ΔCDА по третьему признаку (по трем сторонам), что и требовалось доказать. (Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны).
в) АВ⊥АС, CD⊥AC⇒∡А=∡С=90°, АС-общая, АВ=CD -по условию.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны-первый признак равенства треугольников, значит ΔABC=ΔCDА, что и требовалось доказать.
с) АС-общая, ∡DAC=∡CAB, ∡DCA=∡ACB, так как по условию АС-биссектриса ∡А и ∡С. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны-второй признак равенства треугольников. Значит ΔABC=ΔCDА, что и требовалось доказать.