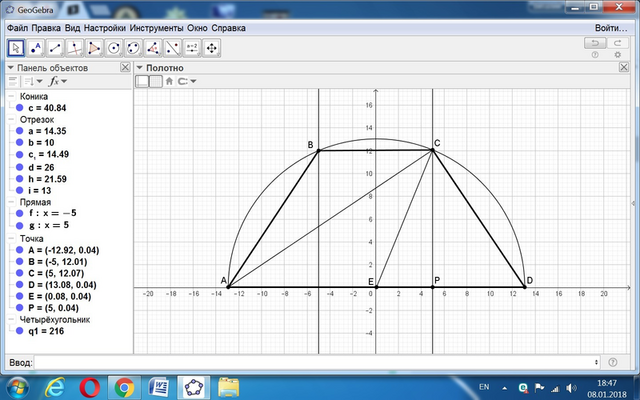
Пусть середина нижнего основания - точка Е, проекция точки С на АД - точка Р.
По свойству прямоугольного треугольника АСД медиана СЕ равна половине гипотенузы АД, то есть СЕ = 26/2 = 13.
Отрезок ЕР равен половине верхнего основания: ЕР = 10/2 = 5.
Находим высоту трапеции С:
СР = √(СЕ² - ЕР²) = √(169 - 25) = √144 = 12.
Отрезок РД равен половине разности оснований: РД = (26 + 10)/2 = 8.
Находим искомую величину тангенса острого угла трапеции:
tg D = CP/PD = 12/8 = 3/2.