Построить график функции y=2/(x^2-4)

Question

Дано ответов: 2

Правильный ответ

$y= \frac{2}{x^2-4}$
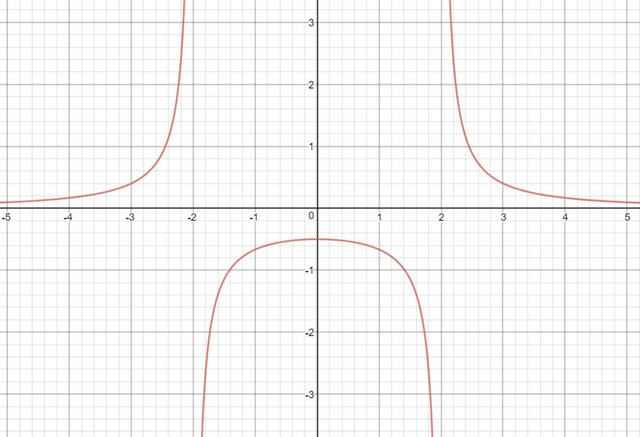
графиком будет гипербола
найдем асимптоты:
нули знаменателя - вертикальные асимптоты:
x^2-4=0
x^2=4
x1=2
x2=-2
x=2 и x=-2 - 2 асимптоты
горизонтальные асимптоты - предел функции, при x->+oo или x->-oo
$\lim_{x \to \infty} \frac{2}{x^2-4}= \frac{2}{\infty} =0$
y=0 - 1 горизонтальная асимптота
у функции нет точек пересечения с осями
найдем производную:
$y'=2*( \frac{1}{x^2-4} )'=2* \frac{0-2x*1}{(x^2-4)^2} =- \frac{4x}{(x^2-4)^2}$
экстремиумы:
-4x=0
x=0
y=-0,5
определим промежутки возрастания/убывания:
так как (x^2-4)^2 знак не меняет, можно ее не учитывать, но при x=2 и x=-2 данное выражение не имеет смысла
-4x>=0 при x<=0 и x≠-2<br>-4x<=0 при x>=0 и x≠2
функция возрастает на (-∞;-2)∪(-2;0]
и убывает на [0;2)∪(2;+∞)
найдем дополнительные точки:
x=-3; y=0,4 (-3;0,4)
x=3; y=0,4 (3;0,4)
x=-1; y=-2/3 (-1;-2/3)
x=1; y=-2/3 (1;2/3)
строим график(см. приложение )

AnonimusPro_zn (149k баллов) 28 Май, 18

sedinalana_zn · Answer 1 · 2018-05-28T01:55:30+0000

Y=2/(x²-4)
D(y)∈(-∞;-2) U (-2;2) U (2;∞)
x=-2 и x=2-вертикальные асимптоты
y(-x)=2/((-x)²-4)=2/(x²-4) четная
y`=-2*2x/(x²-4)^2=0
-4x=0
x=0
+ _ _ +
-------(-2)----------(0)---------(2)------
возр убыв убыв возр

y``(x)=(-4(x²-4)²-2(x²-4)(2x*(-4x))/(x²-4)^4=-4(x²-4)(x²-4-4x²)/(x²-4)^4=
=4(x²-4)(3x²+4)/(x²-4)³=4(3x²+4)/(x²-4)³
точек перегиба нет