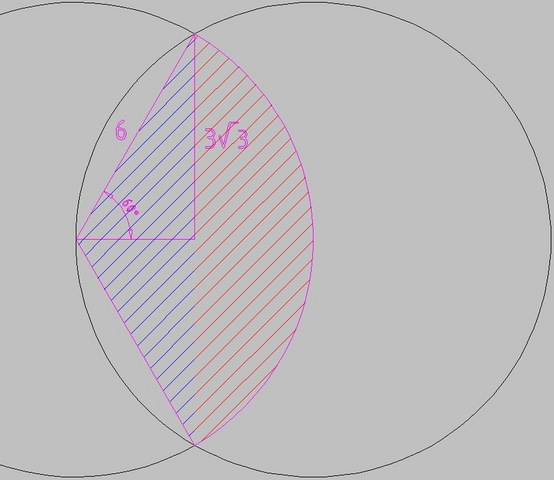
Найдём расстояние между центрами кругов.
Пусть h - половина хорды между точками пересечения
a - расстояние от центра круга до хорды
h = 6√3/2 = 3√3
r² = a² + h²
6² = a² + 9*3
36 = a² + 27
a² = 9
a = 3
а расстояние между центрами кругов равно их радиусу
2a = r
площадь фигуры пересечения будет равна удвоенному красному сектору.
А красный - в свою очередь равен круговому сектору минус синий треугольник
Половинка угла кругового сектора составит
sin(α/2) = 3√3/6 = √3/2
α/a = arccos (√3/2) = π/3
α = 2π/3
Площадь кругового сектора
S₁ = α*r²/2 = 2π/3*6²/2 = 12π
Площадь синего треугольника
S₂ = 1/2*r²*sin(2π/3) = 1/2*36*√3/2 = 9√3
Площадь одного красного сектора
S₃ = S₁ - S₂ = 12π - 9√3
И площадь фигуры пересечения двух кругов
S₄ = 2*S₃ = 24π - 18√3 ≈ 44,2247