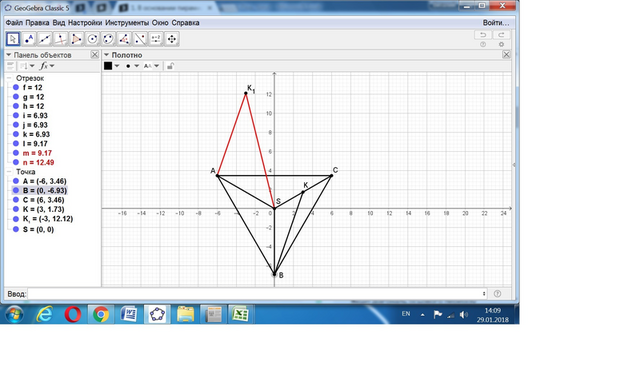
1) Угол, который образует боковая грань пирамиды с плоскостью её основания, зависит не от размеров основания, а от положения вершины.
Максимальный угол боковой грани будет равен 90 градусов в случае, если проекция вершины на основание попадает на одну из сторон основания.
Ответ: максимальный угол боковой грани равен 90 градусов.
2) Дано:площадь боковой грани правильной треугольной пирамиды SABC равна 24, а площадь Sо её основания равна 36√3.
Так как Sо = а²√3/4, то отсюда находим сторону а основания:
а = √(4Sо/√3)= √((4*36√3)/√3) = 2*6 = 12.
Периметр Р = 3а = 3*12 = 36.
Площадь Sбок боковой поверхности правильной треугольной пирамиды SABC равна 3*24 = 72.
Sбок = (1/2)PA.
Апофема А = 2Sбок/Р = 2*72/36 = 4.
Находим длину L бокового ребра:
L = √(A² + (a/2)²) = √(16 + 36) = √52 = 2√13.
Высота Н пирамиды равна:
Н = √(L² - ((2/3)*(a√3/2))²) = √(52 - 48) = √4 = 2.
Так как точка K находится на середине бокового ребра, то высота её hk от основания равна половине Н: hk = 2/2 = 1.
Определим длину отрезка ВК как сторону треугольника SBC:
BK = √(а² + (L/2)² - 2*а*(L/2)*cos(SCB)).
Косинус угла SCB находим так:
cos(SCB) = (a/2)/L = 6/(2√13) = 3/√13 = 3√13/13.
Тогда ВК = √(144 + 13 - 2*12*√13*(3/√13)) = √85.
Для определения угла между скрещивающимися прямыми сделаем параллельный перенос отрезка ВК точкой В в точку А.
Получаем треугольник AK₁S. где AK₁ равно ВК.
Осталось найти длину отрезка K₁S.
Проекция K₁S на плоскость основания равна:
K₂О = √((5√3+2√3)² + 3²)² = √(147 + 9) = √156 = 2√39.
Длина K₁S равна:
K₁S = √(156 + 1) = √157 ≈ 12,52996.
Искомый угол между прямыми BK и AS находим по теореме косинусов.
cos(BK∧AS) = ((4√3)² + (√85)² - (√157)²)/(2*(4√3)*√85) = -0,18786729.
Этому косинусу соответствует угол
1,759787 радиан или
100,828348°.