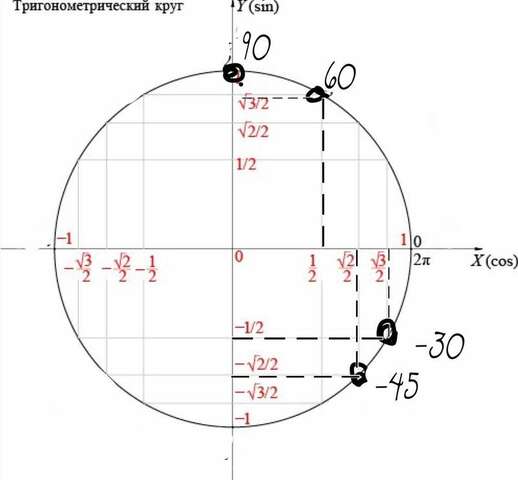
а) рассмотрим прямоугольный треугольник с острыми углами 30 и 60 градусов. В таком треугольнике катет, противолежащий углу 30 градусов и прилежащий углу 60, равен половине гипотенузы, то есть cos60=1/2,т.к косинус- это отношение прилежащего катета к гипотенузе. Пусть этот катет равен х, тогда гипотенуза равна 2х.
Катет, противолежащий углу 60 градусов, по теореме Пифагора равен

, тогда sin60=√3x/2x=√3/2.
b) Рассмотрим прямоугольный треугольник с острыми углами 45 градусов, это равнобедренный прямоугольный треугольник, его катеты равны, значит, можем найти гипотенузу по теореме Пифагора. Пусть катеты равны х, тогда гипотенуза равна

.

.
d)sin30=cos60=1/2, cos30=sin60=√3/2