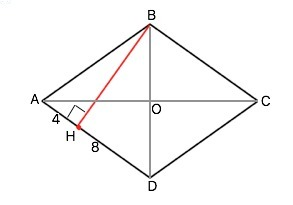
Обозначим вершины ромба АВСD; перпендикуляр, проведенный из В – ВН; по условию АН=4 см, HD=8 см.⇒
AB=AD=4+8=12
Найдем по т.Пифагора
ВН=√(AB²-AH²)=√(144-16)=√128
BH=8√2
Из ∆ ВНD по т.Пифагора
диагональ ВD=√(BH²+DH²)=√192=8√3
Обозначим точку пересечения диагоналей О.
Диагональ АС=2АО
BO=BD:2=4√3
Из ∆ АВО по т.Пифагора
АО=√(AB²-BO²)=√96=4√6⇒
AC=8√6
Диагонали ромба 8√3 см и 8√6 см