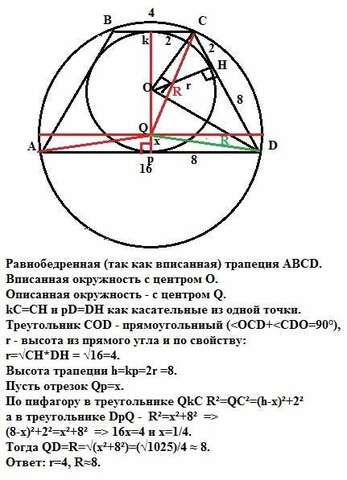
Равнобедренная (так как вписанная) трапеция ABCD.
Вписанная окружность с центром О.
Описанная окружность - с центром Q.
kC=CH=2 и pD=DH=8 как касательные из одной точки.
Треугольник COD - прямоугольниый (r - высота из прямого угла и по свойству:
r=√CH*DH = √16=4.
Высота трапеции h=kp=2r =8.
Пусть отрезок Qp=x.
По пифагору в треугольнике QkC R²=QC²=(h-x)²+2²
а в треугольнике DpQ - R²=x²+8² =>
(8-x)²+2²=x²+8² => 16x=4 и х=1/4.
Тогда QD=R=√(x²+8²)=(√1025)/4 ≈ 8,0039.
Ответ: r=4, R≈8.
P.S. Для проверки. Формула для вычисления радиуса описанной окружности (из интернета):
R=√[(ab+c²)/(4-((b-a)/c)²).
Здесь а- большее основание, b -меньшее основание, с - боковая сторона. Тогда в нашем случае:
R=√[(64+100)/(4-(12/10)²)]=√(164/2,56)=√64,0625 = 8,0039.