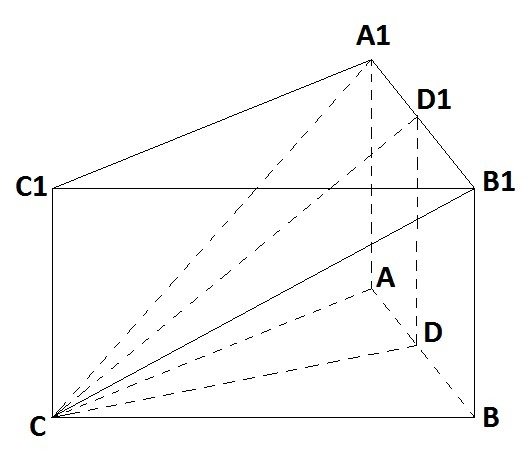
(см. рис.)
Рассмотрим треугольники CBB1 и CAA1:
1) AC=BC по условию
2) AA1=BB1 и ∠CAA1=∠CBB1, т.к. призма прямая.
По первому признаку равенства треугольников ΔCAA1=ΔCBB1.
Так как CA1=CB1, треугольник CA1B1 равнобедренный.
Проведём высоты CD и CD1 в треугольниках CBA и CB1A1. Т.к. эти треугольники равнобедренные, высоты разделят основания пополам, т.е. AD=DB, A1D1=D1B1.
Треугольник CBD прямоугольный, BC - гипотенуза. По т.Пифагора
CD = √(BC²-BD²) = √(10-1) = √9 = 3.
DD1 = AA1 = BB1 = 3, т.к. DD1 - средняя линия прямоугольника AA1BB1.
Треугольник CDD1 прямоугольный, т.к. призма прямая (грани перпендикулярны), CD1 - гипотенуза
По определению тангенса
tg(∠DCD1) = DD1:CD = 3:3 = 1
Значит угол между плоскостью CA1B1 и плоскостью основания
∠DCD1 = arctg(1) = 45 градусов.