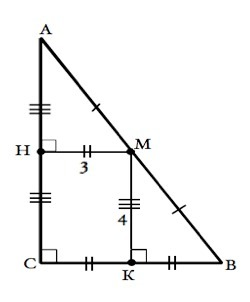
Обозначим треугольник АВС, угол С=90°, т. М - середина гипотенузы.
Расстояние от точки до прямой равно длине проведенного к ней перпендикуляра.
Тогда перпендикуляр МН - расстояние от М до катета АС и параллельно ВС. МН=3 - средняя линия ∆ АВС. ⇒
ВС=2•МН=6 см.
Перпендикуляр МК- расстояние от М до катета ВС и параллельно АС. МК - средняя линия ∆ АВС. ⇒
АС=2• МК=8 см.
Площадь прямоугольного треугольника равна половине произведения катетов.
Ѕ=ВС•АС:2=6•8:2=24 см²