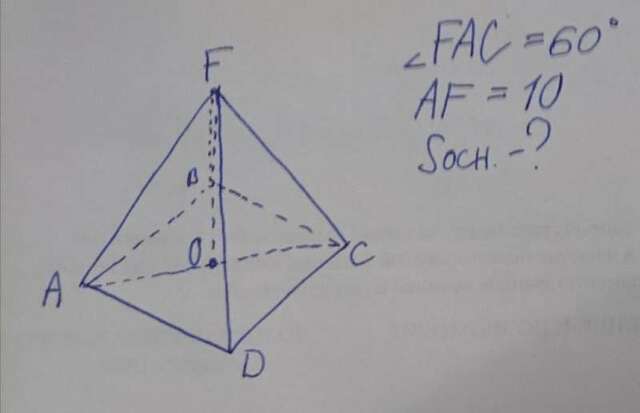
1. Проведём высоту FO. ΔAFO - прямоугольный.
∠AFO = 90° - ∠FAO = 30°
Напротив угла в 30° лежит катет в два раза меньше гипотенузы, то есть 2AO = AF ⇒ AO = 5
Пирамида правильная, поэтому O - точка пересечений диагоналей BD и AC, а AO - половина диагонали AC, так как ABCD - квадрат.
Отсюда AC = 10
Обозначим за x сторону квадрата и из ΔACD по теореме Пифагора найдём эту сторону.
x² + x² = 100
x² = 50
x = √50
Sосн = a² = x² = 50
Ответ: 50
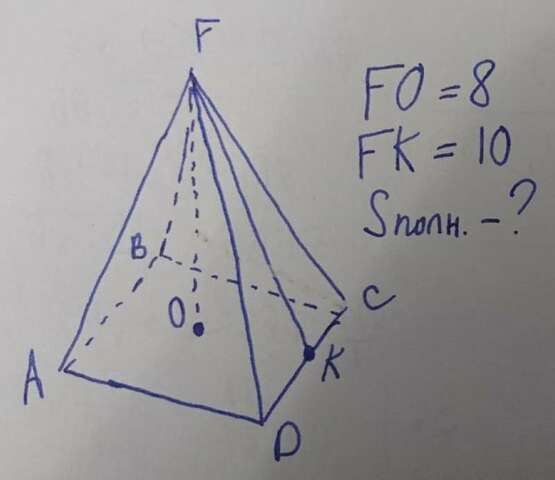
2. Проведём высоту FO и апофему FK. O и K соединим.
ΔOFK - прямоугольный. По теореме Пифагора находим OK:
OK² + FO² = FK²
OK² = 100 - 64
OK² = 36
OK = 6
Пирамида правильная, поэтому точка О - центр квадрата, а OK - половина AD, откуда AD = 12
Sполн = 4 * Sбок.ст. + Sосн = 4 * 1/2FK*DC + AD² = 2 * 10 * 12 + 144 = 384
Ответ: 384