|x|-2x+1/|3-x|=1
ОДЗ х - не равно 3
решается методом интервалов
числовая ось разбивается на участки особыми точками, на каждом участке раскрываются модули и решается уравнение
в нашем случае это точки х=0 и х=3
1) при х<=0 <br>|x|-2x+1/|3-x|=1
-x-2x+1/(3-x)=1
-3x+1/(3-x)=1
-9x+3x^2+1=3-x
3x^2-8x-2=0
корни (4-КОРЕНЬ(22))/3 и (4+КОРЕНЬ(22))/3
(4-КОРЕНЬ(22))/3 принадлежат участку х<=0 <br>2) при 0<х<3<br>|x|-2x+1/|3-x|=1
x-2x+1/(3-x)=1
-x+1/(3-x)=1
-3x+x^2+1=3-x
x^2-2x-2=0
корень 1+ корень(3) принадлежат участку 0<х<3<br>3) при х>3
|x|-2x+1/|3-x|=1
x-2x-1/(3-x)=1
-x-1/(3-x)=1
-3x+x^2-1=3-x
x^2-2x-4=0
корень 1+ корень(5) принадлежат участку 3<х<br>
ответ (3 точки)
x1=(4-КОРЕНЬ(22))/3
x2=корень 1+ корень(3)
x3= корень 1+ корень(5)
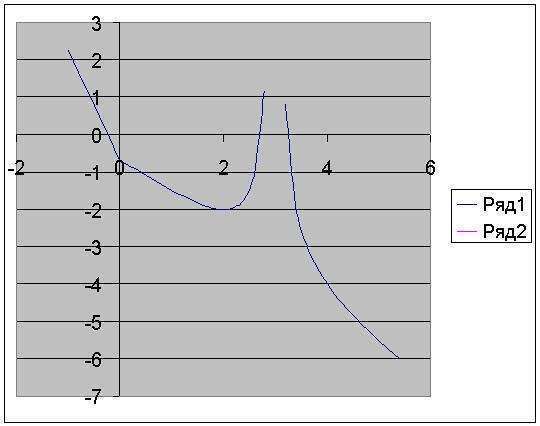
в прикрепленном файле приводится зависимость
y=|x|-2x+1/|3-x|-1
точки пересечения с осью икс - искомые