Найти точки экстремума функции: y= 5x^3-7x^2+2

$y=5x^3-7x^2+2\\y'=15x^2-14x\\15x^2-14x=0\\x(15x-14)=0\\ \left \{ {{x=0} \atop {x= \frac{14}{15} }} \right.\\$
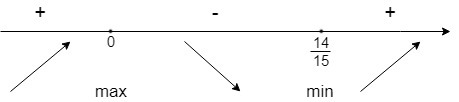
Отмечаем получившиеся точки на числовой прямой. Для определения знака производной достаточно взять по точке на каждом из интервалов:
(-∞;0] ∪ [0; $\frac{14}{15}$ ] ∪ [ $\frac{14}{15}$ ;∞].
y'(1) для промежутка [ $\frac{14}{15}$ ;∞], подставляем в производную - y'.
y'(1) > 0 ⇒ крайний правый промежуток имеет знак " + ".
Аналогично для двух других...

Точка 0 - максимум.
Точка $\frac{14}{15}$ - минимум.